2025.9
信道能用Kronecker表示的前提条件:
Validity of the Kronecker Model for MIMO Correlated Channels
一端的两个天线单元接收到从另一端的任意同一个天线单元的信道的相关系数相同,即要满足:天线间距较小:空间相关性高,信号经历的散射环境相似,因此MIMO规模较小相同的辐射方向图(radiation pattern):天线的增益和辐射特性一致相同的朝向(orientation):极化方向和主瓣方向对齐
联合角度谱可分离每条径的 AoD 和 AoA 之间无特定耦合关系(某个 AoD 不倾向于对应特定 AoA)
在消声室中重建每个簇的PAS,预衰落信号合成法
Emulating Spatial Characteristics of MIMO Channels for OTA Testing
PAS包括平均AOA,以及AS每个簇映射到几个OTA探头,给探头分配合适的功率权重来重建目标信道的空间特征(即簇的PAS)由于DUT的天线方向图是未知的,对于测试区域任意两个采样单元假设是全向的,两个单元组成线阵列, ...
基本思想:将阵列输出信号的协方差矩阵进行特征分解,根据特征值的大小划分信号子空间和噪声子空间,利用二者的正交性估计信号的来波方向
MIMO信号传输公式Y(t)=A(\theta )X(\theta ,t)将M个阵元在t时刻接收的信号排列成一个列矢量,记为Y(t)\in \mathbb{C} ^{M\times 1},N条径排成列矢量X(\theta,t)\in \mathbb{C} ^{N\times 1}当确定阵列形状,可以得到阵列传输矩阵A(\theta )\in \mathbb{C} ^{M\times N} ,A(\theta )=[\alpha _{1} ,\alpha _{2},\dots ,\alpha _{N} ],其中\alpha _{i}表示第i个入射波到达阵元的导向矢量MUSIC(Multiple Signal classification)算法就是估计信道的空间特性,即多径的角度
假设
信号源数N小于阵元的数目M,以确保A列满秩
信号源通常为窄带远场信号(多径,平面波模型,每条径都是随机变量)
不同径是独立的
算法推导对于Y,协方差矩阵R\in \mathb ...
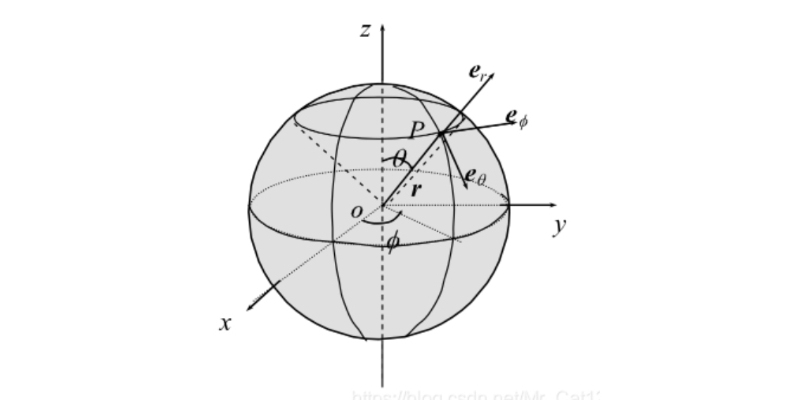
单位矢量关于\overline{e_{r}} , \overline{e_{\theta }} ,\overline{e_{\varphi }} 和\overline{e_{x}} , \overline{e_{y}} ,\overline{e_{z }}的转化
[{"url":"https://bu.dusays.com/2025/09/05/68bac3c5239f3.png","alt":""},{"url":"https://bu.dusays.com/2025/09/05/68bac3e6d2f5d.jpg","alt":""}]
加载更多
立体角定义:投影面积与球的半径平方之比面积微元dA:dA=rd\theta \cdot rsin\theta d\varphi
d\Omega =\frac{dA}{r^{2} } =sin\theta d\theta d\varphi\int _{A} d\Omega =\int_{0}^{2\pi } d\varphi \int_{0}^{\pi } sin\theta d\theta =4\p ...
\frac{\partial(\boldsymbol{x}^T \boldsymbol{a})}{\partial \boldsymbol{x}} = \frac{\partial(\boldsymbol{a}^T \boldsymbol{x})}{\partial \boldsymbol{x}} = \boldsymbol{a}其中,$\boldsymbol{a}$ 为常数向量,$\boldsymbol{a} = (a_1, a_2, \cdots, a_n)^T$ 证明
\frac{\partial(\boldsymbol{x}^T \boldsymbol{a})}{\partial \boldsymbol{x}} = \frac{\partial(\boldsymbol{a}^T \boldsymbol{x})}{\partial \boldsymbol{x}}= \frac{\partial(a_1 x_1 + a_2 x_2 + \cdots + a_n x_n)}{\partial \boldsymbol{x}}= ...
123import numpy as npimport pandas as pdimport matplotlib.pyplot as plt
pandas加载数据到DataFrame:
path = ‘ex1data1.txt’ # 创建字符串变量
data = pd.read_csv(path, header=None, names=[‘Population’, ‘Profit’]) #header:文件本身的列标题行,为none即第一行就是数据
12data.head() #显示DataFrame的前5行data.describe() #自动计算各列统计值
绘图12data.plot(kind='scatter', x='Population', y='Profit', figsize=(10,6))\plt.show() #显示图形
数据集插入一列1data.insert(0, 'Ones', 1) #对date这个DataFrame在第一列插入新列,名称Ones,值为1
num ...
size12size(A)%返回一个行向量,该行向量的第一个元素是矩阵的行数,第二个元素是矩阵的列数size(A,a)%a=1,返回行数;a=2,返回列数
meshgrid代码输出123a = [1 2 3 4];b = [5 6 7 8];[A,B] = meshgrid(a,b)%a做为行下拉复制,b作为列右拉复制123456789101112131415A = 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4B = 5 5 5 5 6 6 6 6 7 7 7 7 8 8 8 8
reshape代码输出12A=[1 2 3; 4 5 6]A_vec=reshape(A,[],1)123456789A_vec = 1 4 2 5 3 6
Q&A
Explain multi-probe anechoic chamber principle
用多个探头来模拟PAS对于毫米波,天线电子尺寸大,主瓣变窄,对空间角度分辨率提高,要更多探头以及连在后面的channel emulator(CE很贵)
Explain radiated two stage method principle
CE里不仅有H还有A逆来消除A的影响,H里还包含了天线所以叫two stage
Explain radiated wireless cable method principleCE发射的信号在一个消声盒子里传到DUT,会产生矩阵A,原本CE是通过RFcable直接连到DUT测试DUT性能,但现在DUT里天线是高度集成的,不能用cable了,所以叫wireless cableradiated two stage method的第二步
Wireless Communications
未读Q&A
Explain basic structure of MIMO and SISO channel modelSISO:TX一个天线,Rx一个天线MIMO:TX多个天线,Rx多个天线
Explain basic double-directional channel model concept
多了AOA,AOD体现空间上的变化
Explain basic concept of channel cluster
相似时延和到达角的多径分量集合
Explain 3GPP 38.901 channel model Table 7.7.1-1. CDL-ACDL-A
Clustered Delay Line
没有直达径
簇个数,每个簇的normalized delay,power,AOD,AOA,ZOD,ZOA,角扩展,XPR
Explain basic correlation-based channel modelTx有M个天线,Rx有N的天线,根据测得的PAS做傅里叶变换得到每端空间相关函数,做克罗内克积,得到MNXMN矩阵R,这是一个正定矩阵,做分解,得到 ...
测量参数powerdoppler spectrumdelay spectrumspatial spectrum(AOA)polarization(接收机先放水平极化天线,再放垂直极化天线,信道极化信息就拿到了)
power
narrowband测量只测能量,接收端放一个仪器
power mater(narrowband)
spectrum analyzer(从频谱看每点能量)有small scale fading,测power是不关注的,需要去掉,在一块区域里移动接收端,对测到的power取平均
wideband测量可以区分多径,看到每个时延的能量,将能量相加,避免了small scale fading
doppler spectrum得是窄带系统时域采样满足奈奎斯特采样定理,即 f(采样点/s)\ge 2f_{m} (最大多普勒频移)发一个CW(单音)信号,用spectrum analyzer拿到多普勒谱
delay spectrumimpulse channel sounder发送窄脉冲,直接测量接收端的多径响应问题:所有能量集中在非常窄的脉冲,贵,能量受限
frequency ...
Q&A
Explain what is radio channel and why radio channel modeling is important?Radio channel:propagation channel(环境)+antennaImportant:
需要知道信道来处理信息
信道是无线通信重要组成部分
唯一无法被控制的成分(5G之前,现在有RIS)
知道信道性能对系统,算法,天线设计至关重要
Narrowband channel, how it is modeled and explain its components.路径损耗(与d有关)+大尺度衰落(对数正态分布)+小尺度衰落(rayleigh/rice…distribution)
Explain Free-space path loss, explain why mmWave frequency was regarded as “junk frequency” bank for cellular communication early days and how the concerns are ha ...